Nature in Numbers [EVERYTHING IS PHI!]

Fibonacci Numbers and Nature

Before anything, check this video :)

Rabbits, Cows and Bees Family Trees

Let's look first at the Rabbit Puzzle that Fibonacci wrote about and then at two adaptations of it to make it more realistic. This introduces you to the Fibonacci Number series and the simple definition of the whole never-ending series.

Fibonacci's Rabbits

The original problem that Fibonacci investigated (in the year 1202) was about how fast rabbits could breed in ideal circumstances.

Suppose a newly-born pair of rabbits, one male, one female, are put in a field. Rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits. Suppose that our rabbits never die and that the female always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was...
How many pairs will there be in one year?

1. At the end of the first month, they mate, but there is still one only 1 pair.
2. At the end of the second month the female produces a new pair, so now there are 2 pairs of rabbits in the field.
3. At the end of the third month, the original female produces a second pair, making 3 pairs in all in the field.
4. At the end of the fourth month, the original female has produced yet another new pair, the female born two months ago produces her first pair also, making 5 pairs.

The number of pairs of rabbits in the field at the start of each month is 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

Can you see how the series is formed and how it continues? If not, look at the answer!
The first 300 Fibonacci numbers are here and some questions for you to answer.
Now can you see why this is the answer to our Rabbits problem? If not, here's why.
Another view of the Rabbit's Family Tree:
Both diagrams above represent the same information. Rabbits have been numbered to enable comparisons and to count them, as follows:

• All the rabbits born in the same month are of the same generation and are on the same level in the tree.
• The rabbits have been uniquely numbered so that in the same generation the new rabbits are numbered in the order of their parent's number. Thus 5, 6 and 7 are the children of 0, 1 and 2 respectively.
• The rabbits labelled with a Fibonacci number are the children of the original rabbit (0) at the top of the tree.
• There are a Fibonacci number of new rabbits in each generation, marked with a dot.
• There are a Fibonacci number of rabbits in total from the top down to any single generation.

There are many other interesting mathematical properties of this tree that are explored in later pages at this site.

The Rabbits problem is not very realistic, is it?

It seems to imply that brother and sisters mate, which, genetically, leads to problems. We can get round this by saying that the female of each pair mates with any male and produces another pair.
Another problem which again is not true to life, is that each birth is of exactly two rabbits, one male and one female.

Dudeney's Cows

The English puzzlist, Henry E Dudeney (1857 - 1930, pronounced Dude-knee) wrote several excellent books of puzzles (see after this section). In one of them he adapts Fibonacci's Rabbits to cows, making the problem more realistic in the way we observed above. He gets round the problems by noticing that really, it is only the females that are interesting - er - I mean the number of females!
He changes months into years and rabbits into bulls (male) and cows (females) in problem 175 in his book 536 puzzles and Curious Problems (1967, Souvenir press):

If a cow produces its first she-calf at age two years and after that produces another single she-calf every year, how many she-calves are there after 12 years, assuming none die?

This is a better simplification of the problem and quite realistic now.
But Fibonacci does what mathematicians often do at first, simplify the problem and see what happens - and the series bearing his name does have lots of other interesting and practical applications as we see later.
So let's look at another real-life situation that is exactly modelled by Fibonacci's series - honeybees.

Puzzle books by Henry E Dudeney

Amusements in Mathematics, Dover Press, 1958, 250 pages.
Still in print thanks to Dover in a very sturdy paperback format at an incredibly inexpensive price. This is a wonderful collection that I find I often dip into. There are arithmetic puzzles, geometric puzzles, chessboard puzzles, an excellent chapter on all kinds of mazes and solving them, magic squares, river crossing puzzles, and more, all with full solutions and often extra notes! Highly recommended!
536 Puzzles and Curious Problems is now out of print, but you may be able to pick up a second hand version by clicking on this link. It is another collection like Amusements in Mathematics (above) but containing different puzzles arranged in sections: Arithmetical and Algebraic puzzles, Geometrical puzzles, Combinatorial and Topological puzzles, Game puzzles, Domino puzzles, match puzzles and "unclassified" puzzles. Full solutions and index. A real treasure.
The Canterbury Puzzles, Dover 2002, 256 pages. More puzzles (not in the previous books) the first section with some characters from Chaucer's Canterbury Tales and other sections on the Monks of Riddlewell, the squire's Christmas party, the Professors puzzles and so on and all with full solutions of course!

Honeybees and Family trees

There are over 30,000 species of bees and in most of them the bees live solitary lives. The one most of us know best is the honeybee and it, unusually, lives in a colony called a hive and they have an unusual Family Tree. In fact, there are many unusual features of honeybees and in this section we will show how the Fibonacci numbers count a honeybee's ancestors (in this section a "bee" will mean a "honeybee").
First, some unusual facts about honeybees such as: not all of them have two parents!

• In a colony of honeybees there is one special female called the queen.
• There are many worker bees who are female too but unlike the queen bee, they produce no eggs.
• There are some drone bees who are male and do no work.
  Males are produced by the queen's unfertilised eggs, so male bees only have a mother but no father!
• All the females are produced when the queen has mated with a male and so have two parents. Females usually end up as worker bees but some are fed with a special substance called royal jelly which makes them grow into queens ready to go off to start a new colony when the bees form a swarm and leave their home (a hive) in search of a place to build a new nest.

So female bees have 2 parents, a male and a female whereas male bees have just one parent, a female.
Here we follow the convention of Family Trees that parents appear above their children, so the latest generations are at the bottom and the higher up we go, the older people are. Such trees show all the ancestors (predecessors, forebears, antecedents) of the person at the bottom of the diagram. We would get quite a different tree if we listed all the descendants (progeny, offspring) of a person as we did in the rabbit problem, where we showed all the descendants of the original pair.
Let's look at the family tree of a male drone bee.

1. He had 1 parent, a female.
2. He has 2 grand-parents, since his mother had two parents, a male and a female.
3. He has 3 great-grand-parents: his grand-mother had two parents but his grand-father had only one.
4. How many great-great-grand parents did he have?

Again we see the Fibonacci numbers :

                                       great-     great,great   gt,gt,gt
                           grand-      grand-     grand         grand
Number of       parents:   parents:    parents:   parents:      parents:
of a MALE bee:    1           2           3          5             8
of a FEMALE bee:  2           3           5          8            13
  

The Fibonacci Sequence as it appears in Nature by S.L.Basin in Fibonacci Quarterly, vol 1 (1963), pages 53 - 57.

Things to do

1. Make a diagram of your own family tree. Ask your parents and grandparents and older relatives as each will be able to tell you about particular parts of your family tree that other's didn't know. It can be quite fun trying to see how far back you can go. If you have them put old photographs of relatives on a big chart of your Tree (or use photocopies of the photographs if your relatives want to keep the originals). If you like, include the year and place of birth and death and also the dates of any marriages.
2. A brother or sister is the name for someone who has the same two parents as yourself. What is a half-brother and half-sister?
   Describe a cousin but use simpler words such as brother, sister, parent, child?
   Do the same for nephew and niece. What is a second cousin? What do we mean by a brother-in-law, sister-in-law, mother-in-law, etc? Grand- and great- refer to relatives or your parents. Thus a grand-father is a father of a parent of yours and great-aunt or grand-aunt is the name given to an aunt of your parent's.Make a diagram of Family Tree Names so that "Me" is at the bottom and "Mum" and "Dad" are above you. Mark in "brother", "sister", "uncle", "nephew" and as many other names of (kinds of) relatives that you know. It doesn't matter if you have no brothers or sisters or nephews as the diagram is meant to show the relationships and their names.
   [If you have a friend who speaks a foreign language, ask them what words they use for these relationships.]
3. What is the name for the wife of a parent's brother?
   Do you use a different name for the sister of your parent's?
   In law these two are sometimes distinguished because one is a blood relative of yours and the other is not, just a relative through marriage.
   Which do you think is the blood relative and which the relation because of marriage?
4. How many parents does everyone have?
   So how many grand-parents will you have to make spaces for in your Family tree?
   Each of them also had two parents so how many great-grand-parents of yours will there be in your Tree?
   ..and how many great-great-grandparents?
   What is the pattern in this series of numbers?
   If you go back one generation to your parents, and two to your grand-parents, how many entries will there be 5 generations ago in your Tree? and how many 10 generations ago?The Family Tree of humans involves a different sequence to the Fibonacci Numbers. What is this sequence called?
5. Looking at your answers to the previous question, your friend Dee Duckshun says to you:
   • You have 2 parents.
   • They each have two parents, so that's 4 grand-parents you've got.
   • They also had two parents each making 8 great-grand-parents in total ...
   • ... and 16 great-great-grand-parents ...
   • ... and so on.
   • So the farther back you go in your Family Tree the more people there are.
   • It is the same for the Family Tree of everyone alive in the world today.
   • It shows that the farther back in time we go, the more people there must have been.
   • So it is a logical deduction that the population of the world must be getting smaller and smaller as time goes on!
   Is there an error in Dee's argument? If so, what is it? Ask your maths teacher or a parent if you are not sure of the answer!

Fibonacci numbers and the Golden Number

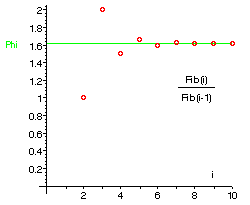
If we take the ratio of two successive numbers in Fibonacci's series, (1, 1, 2, 3, 5, 8, 13, ..) and we divide each by the number before it, we will find the following series of numbers:
¹/₁ = 1,   ²/₁ = 2,   ³/₂ = 1·5,   ⁵/₃ = 1·666...,   ⁸/₅ = 1·6,   ¹³/₈ = 1·625,   ²¹/₁₃ = 1·61538...
It is easier to see what is happening if we plot the ratios on a graph:

The ratio seems to be settling down to a particular value, which we call the golden ratio or the golden number. It has a value of approximately 1·618034 , although we shall find an even more accurate value on a later page [this link opens a new window] .

Things to do

• What happens if we take the ratios the other way round i.e. we divide each number by the one following it: 1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ..?
  Use your calculator and perhaps plot a graph of these ratios and see if anything similar is happening compared with the graph above.
  You'll have spotted a fundamental property of this ratio when you find the limiting value of the new series!

The golden ratio 1·618034 is also called the golden section or the golden mean or just the golden number. It is often represented by a Greek letter Phi . The closely related value which we write as phi with a small "p" is just the decimal part of Phi, namely 0·618034.

Fibonacci Rectangles and Shell Spirals

We can make another picture showing the Fibonacci numbers 1,1,2,3,5,8,13,21,.. if we start with two small squares of size 1 next to each other. On top of both of these draw a square of size 2 (=1+1).
We can now draw a new square - touching both a unit square and the latest square of side 2 - so having sides 3 units long; and then another touching both the 2-square and the 3-square (which has sides of 5 units). We can continue adding squares around the picture, each new square having a side which is as long as the sum of the latest two square's sides. This set of rectangles whose sides are two successive Fibonacci numbers in length and which are composed of squares with sides which are Fibonacci numbers, we will call the Fibonacci Rectangles.
Here is a spiral drawn in the squares, a quarter of a circle in each square. The spiral is not a true mathematical spiral (since it is made up of fragments which are parts of circles and does not go on getting smaller and smaller) but it is a good approximation to a kind of spiral that does appear often in nature. Such spirals are seen in the shape of shells of snails and sea shells and, as we see later, in the arrangement of seeds on flowering plants too. The spiral-in-the-squares makes a line from the centre of the spiral increase by a factor of the golden number in each square. So points on the spiral are 1.618 times as far from the centre after a quarter-turn. In a whole turn the points on a radius out from the centre are 1.618⁴ = 6.854 times further out than when the curve last crossed the same radial line.

Cundy and Rollett (Mathematical Models, second edition 1961, page 70) say that this spiral occurs in snail-shells and flower-heads referring to D'Arcy Thompson's On Growth and Form probably meaning chapter 6 "The Equiangular Spiral". Here Thompson is talking about a class of spiral with a constant expansion factor along a central line and not just shells with a Phi expansion factor.

Below are images of cross-sections of a Nautilus sea shell. They show the spiral curve of the shell and the internal chambers that the animal using it adds on as it grows. The chambers provide buoyancy in the water. Click on the picture to enlarge it in a new window. Draw a line from the centre out in any direction and find two places where the shell crosses it so that the shell spiral has gone round just once between them. The outer crossing point will be about 1.6 times as far from the centre as the next inner point on the line where the shell crosses it. This shows that the shell has grown by a factor of the golden ratio in one turn.
On the poster shown here, this factor varies from 1.6 to 1.9 and may be due to the shell not being cut exactly along a central plane to produce the cross-section.
Several organisations and companies have a logo based on this design, using the spiral of Fibonacci squares and sometime with the Nautilus shell superimposed. It is incorrect to say this is a Phi-spiral. Firstly the "spiral" is only an approximation as it is made up of separate and distinct quarter-circles; secondly the (true) spiral increases by a factor Phi every quarter-turn so it is more correct to call it a Phi⁴ spiral.
Here are some more posters available from AllPosters.com that are great for your study wall or classroom or to go with a science project. Click on the pictures to enlarge them in a new window.

Nautilus Wampler, Sondra Buy this Art Print at AllPosters.com

Nautilus Shell Myers, Bert Buy this Art Print at AllPosters.com

Nautilus Schenck, Deborah Buy this Art Print at AllPosters.com

The curve of this shell is called Equiangular or Logarithmic spirals and are common in nature, though the 'growth factor' may not always be the golden ratio.

Reference

 The Curves of Life Theodore A Cook, Dover books, 1979, ISBN 0 486 23701 X.
A Dover reprint of a classic 1914 book.

Thanks for reading, please comment :)